LA MODÉLISATION DPSM POUR LA SIMULATION DU VOL

Par Dominique Placko¹, Jean-Pierre Barbot^1,2 et Serge Gourlaouen^1,2

¹Laboratoire SATIE, UMR 8029 (CNRS / ENS Paris-Saclay), 4 Avenue des Sciences, 91190 Gif-sur-Yvette, France.

²FLYNAERO, 43 Avenue Robert Schuman, 94150 Rungis, France.

LA SIMULATION NUMÉRIQUE EN MÉCANIQUE DES FLUIDES

Les outils de conception numériques sont devenus incontournables. Aidées en cela par le développe ment de l’informatique, de l’analyse numérique et par l’accroissement de la puissance de calcul des ordinateurs, la modélisation comme la simulation numérique permettent d’étudier, de concevoir et de reproduire le comportement de systèmes complexes. Si la modélisation s’attache à représenter un phénomène physique par un ensemble d’équations mathématiques permettant d’en rendre le comporte ment global plus accessible et prédictif, la simulation en revanche se consacre à la reproduction point par point de la partie visible du phénomène physique. Ainsi, la modélisation est au cœur du phénomène là où la simulation n’en représente que les effets. 

Dans le cas des simulateurs de vol destinés à la formation des pilotes, l’avion étant un système complexe de par sa mécanique du vol, la contrainte « temps réel » fait que les simulations numériques se cantonnent à représenter le comportement final de l’avion. En revanche, lors des phases de conception des aéronefs, les modèles numériques permettent de prédire les comportements en vol d’une géométrie donnée, phase qui nécessite la réalisation de maquettes et de nombreuses mesures en soufflerie. Bien que la durée des calculs effectués sur de très puissants ordinateurs puisse paraître démesurée, nous parlons de semaines de temps de calcul, l’apport des souffleries numériques que sont les logiciels de CFD (pour Computational Fluid Dynamics) accélère grandement toutes les phases de conception des aéronefs.

 De nombreuses stratégies de modélisation physique existent. Elles ont toutes pour point commun la résolution des équations aux dérivées partielles (EDP) régissant la physique du phénomène étudié mais avec des stratégies de résolution numérique différentes. Parmi ces techniques, la méthode des éléments finis (FEM pour Finit Element Method) [1] est la plus répandue. Toutefois des alternatives existent, la méthode des éléments finis de frontière, (BEM pour Boundary Element Method) par exemple, utilisée quand les domaines modélisés deviennent infinis, et ce qui est le cas pour la mécanique des f luides externes.

La modélisation DPSM (pour Distributed Point Source Method) [2], est issue de travaux menés en instrumentation et en contrôle non-destructif au laboratoire SATIE (UMR 8025, CNRS/ENS Paris Saclay). Appliquée pour modéliser divers domaines de la physique (les ultra-sons, la magnétostatique, l’électromagnétisme), la modélisation DPSM a été étendue à la mécanique des fluides. S’apparentant à la méthode des points singuliers [3] et de type BEM, cette modélisation est parfaitement adaptée à la mécanique des fluides externes. Non itérative, naturellement 3D et ne nécessitant qu’un maillage surfacique, cette modélisation physique se montre pour cet usage significativement plus rapide que la FEM. Intrinsèquement adaptée à la réduction de modèle, la méthode DPSM permet des prédictions physiques en « temps réel » et a été testée avec succès dans la boucle de vol d’un simulateur de vol de type « full flight » [4], [5] [6]. 

MODÉLISATION DPSM ET MÉCANIQUE DES FLUIDES

De façon très générale, l’écoulement d’un fluide massique est décrit par des EDP et en particulier par les équations de Navier-Stokes. Ces dernières sont non linéaires et leur résolution mathématique non garantie. Toutefois, en introduisant des hypothèses fortes, il devient possible de les linéariser et ainsi d’obtenir une solution approchée satisfaisante. Dans l’hypothèse d’un fluide incompressible et non visqueux, la résolution des équations de Naviers Stockes permet d’obtenir la vitesse d’un fluide massique sous forme de deux termes de champ de vitesse. Le premier terme représente les écoulements potentiels, c’est-à-dire ceux dont le champ de vitesse est irrotationnel. Le second au contraire correspond aux écoulements dont le champ de vitesse est purement rotationnel. On retrouve ainsi une analogie forte avec l’électromagnétisme et l’expression de la force de Laplace où la force radiale s’exerçant sur une particule chargée est due au champ électrique, dérivant d’un potentiel et une force rotationnelle due au champ magnétique.

La partie irrotationnelle représentant les écoulements potentiels se traduit dans le cadre de la modélisation DPSM sous forme d’une source radiale (ou scalaire) de fluide massique. Cette émission radiale de fluide, figure 2, va permettre de s’opposer et/ou de modifier la trajectoire du fluide massique global, figure 1. 

 Fig. 1 - Flux de fluide massique traversant une aile (NACA 4424) supposée transparente.

 Fig. 2 - Réaction des sources scalaires (ou radiales) quand l’aile est supposée étanche.

La circulation, et donc la portance, proviennent de la partie purement rotationnelle de la solution, figure 4. Dans le cas d’un fluide massique incompressible et non visqueux, cette circulation traduit la mise en rotation du volume de fluide perturbé par l’avance ment de l’aile à une vitesse donnée. 

Fig. 3 - Effet des sources radiales sur un flux massique orienté suivant Vx (cas d’une aile NACA 4424).

Fig. 4 - Circulation autour de l’aile générée par l’ensemble des sources rotationnelles.

La superposition des composantes radiales et rotationnelles, combinée avec le vent global, f igures 5 et 6, permet de modéliser l’ensemble des phénomènes auxquels une aile est soumise lors de son déplacement dans un fluide.

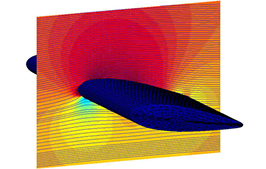
Fig. 5 - Effet des sources radiales et rotationnelles sur un flux massique orienté suivant Vx (cas d’une aile NACA 4424).

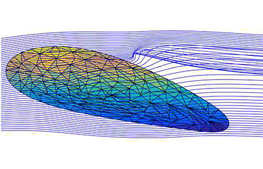
 Fig. 6 - Effet des sources vortex secondaires générant les tourbillons marginaux tribord et bâbord.

 LES ENJEUX DE LA SIMULATION DU VOL

 Pour la conception des aéronefs

Avec l’objectif de construire un avion totalement repensé qui satisfasse aux multiples objectifs que sont la meilleure aérodynamique possible, la minimi sation la consommation, l’utilisation de nouvelles énergies et de ce fait l’intégration de réservoirs poten tiellement plus encombrants, il devient nécessaire de se doter de nouveaux moyens de conception. La modélisation qui est au cœur de ce processus doit prédire rapidement et de façon fiable quelles seront la portance, et donc la capacité de transport, et la trainée, dont est directement dépendante la consommation, d’un objet dont la géométrie évolue paramétriquement. La méthode DPSM est adaptée car cette modélisation est non itérative et ne requiert qu’un maillage surfacique facilement modifiable. Les temps de simulation réduits qu’elle nécessite en font, dans le cas d’une conception p-design [7] et plus généralement dans un scénario de type IA, un excellent noyau de calcul des paramètres aérodyna miques à optimiser [12]. 

 Pour les simulateurs de vol

Le terme de pilotage exprime tant l’action de l’homme sur un système que son contrôle. Ainsi placé au cœur même de la boucle de retour du système complexe qu’est l’avion, le pilote imprime des ordres à la machine et en mesure les effets. Le simulateur de vol, figure 7, doit donc être repré sentatif du comportement de l’avion pour chacune des sollicitations de celui-ci, y compris dans sa composante temporelle. C’est pour cette raison que la restitution de ces composantes de vol s’effectue généralement à partir de tabulations extraites de l’enregistrement du comportement de l’avion simulé lors d’un vol instrumenté. Ainsi, du fait de la contrainte temps réel, il n’y a pas de physique dans la boucle, seulement une restitution du comportement d’un avion lors d’un vol d’essai. Si cette simulation du comportement de l’avion peut sembler satisfai sante lors de certaines phases de vol, elle manque de réalisme lorsque l’avion approche sol, typiquement lors de la simulation des phases de décollage et d’atterrissage [8].

 Fig. 7 - Simulateur de vol de type « full-flight ». Crédit S. Gourlaouen.

 Afin de réintroduire de la physique dans la boucle notamment dans le comportement au voisinage du sol nous avons testé une configuration minimaliste du DPSM dans laquelle l’avion était représenté par un nombre réduit de sources « hybrides », confi guration appelée mini-modèle vectoriel (MMV) [9] [10]. Une source hybride est une source comportant en un même point la superposition d’une source élémentaire scalaire et d’une source rotationnelle.

Pendant cette expérimentation, l’identification des sources avait été possible parce que nous avions accès à certaines données d’essais en vol. Lorsque ces données ne sont pas disponibles, il reste possible de les synthétiser à l’aide du DPSM. En effet, à partir d’un maillage surfacique de l’enveloppe de l’avion, la méthode DPSM permet de modéliser et de prédire les forces et moments s’exerçant sur cette structure lorsque celle-ci est en vol. Il est donc possible d’estimer la valeur des sources du MMV uniquement à partir d’une modélisation DPSM [11]. Ainsi, la simulation MMV permet d’introduire un calcul physique à l’intérieur de la boucle de contrôle d’un simulateur de vol et potentiellement de reproduire de façon plus fidèle le comportement de l’avion dans toutes les situations. 

 PÉRIMÈTRE D’APPLICATION DE LA MÉTHODE DPSM

La méthode DPSM reste valide au-delà de Mach 0.3 où le terme de compressibilité devient non négligeable, voir figures 8 et 9. 

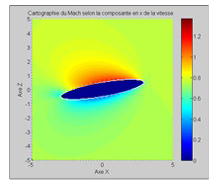
Fig. 8 – Ecoulement à Mach 0.75. Mise en évidence de la MMO via l’accélération des filets d’air en extrados.

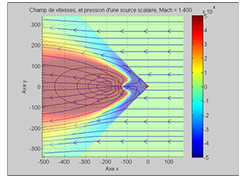
 Fig. 9 – Obstacle ponctuel soumis à un flux d’air à Mach=1.414. Ex : modélisation du calage de l’onde de choc par une souris d’entrée d’air.

 LA MODÉLISATION DPSM POUR LA SIMULATION DU VOL

La rapidité de la méthode DPSM liée à son caractère non-itératif, sa stabilité numérique et le fait qu’elle ne requiert qu’un maillage surfacique, font qu’elle peut tout à fait s’envisager comme noyau de calcul dans un algorithme de type P-design ou d’IA pour la recherche de nouvelles structures d’aéronefs.

Références

[1] [5] Girault V. and Raviart P.-A. ; Finite Element Methods for Navier-Stokes Equations: Theory and Algorithms. Springer Publishing Company, Incorporated, 1st edition, 2011.

[2]  Placko D. and Kundu T. ; DPSM for modeling engineering problems, Wiley-Interscience, 2007.

[3]Gourinat Y. ; La théorie des singularités – Un complement aux modèles locaux par éléments f inis en physique. Techniques de l’ingénieur physique chimie, Vol. Base documentaire TIP053WEB, Editions T.I., 2019.

[4] Placko D. and Barbot J.-P. and Gourlaouen S. and Rivollet A. ; Modélisation en mécanique des f luides par la méthode DPSM : applications aux simulateurs de vol. Conférence invitée, DGAC, Paris, France, juin 2019.

[5] Placko D. and Gourlaouen S. and Rivollet A. and Barbot J.-P. ; Towards real-time aerodynamic simulations. 54 th 3AF Internationnal Inter nationnal on Applied Aerodynamics, Paris, France, March 2019.

[6] Placko D. and Barbot J.-P. and Gourlaouen and Rivollet A. ; Procédé de simulation d’un flux dans lequel est plongée une structure. Brevet EP2019071286W·2019-08-08; FR1857440A·2018 08-10. EP2015061464W·2015-05-22 ; FR1454675A·2014 05-23.

[7] Placko D. and Placko A. and Gourlaouen S. and Barbot J.-P. ; P-design improvement using the DPSM method. 56th 3AF Internationnal Inter nationnal on Applied Aerodynamics, Toulouse, France, March 2022.

[8] [9] Placko D. and Barbot J.-P. and Gourlaouen S. ; Model order reduction, application of the DPSM method to real time flight simulation. 58th 3AF Internationnal Internationnal on Applied Aerodynamics, Orléans, France, March 2024. Placko D. and Gourlaouen S. and Barbot J.-P. and Rivollet A. ; New Approach of Aerodata Computation for Simulation. RAES,

Bristol, UK, July 2018.

[10] Placko D. and Gourlaouen S and and Rivollet A. ; Procédé de simulation de forces f luide. appliquées à une aile dans un écoulement de Brevet FR1750153A·2017-01-06, EP2018050214W·2018-01-04.

[11] Placko D. and Gourlaouen S and and Rivollet A. ; Dispositif et proceed de mesure d’une grandeur physique d’un écoulement de fluide. Brevet [6] Placko D. and Barbot J.-P. and Gourlaouen and Rivollet A. ; Procédé de simulation d’un flux dans lequel est plongée une structure. Brevet EP2019071286W·2019-08-08; FR1857440A·2018 08-10. EP2015061464W·2015-05-22 ; FR1454675A·2014 05-23.

[12] Chambelin J.-P. and Gilliéron P. ; Au-delà du PPL, ISBN 9782383951216, Editions Cépaduès, 2024. LETTRE 3AF 2-2025 / AVRIL - JUIN